參數(shù)資料
型號(hào)： TLC2942PW
廠商： Texas Instruments, Inc.
英文描述： HIGH-PERFORMANCE DUAL PHASE-LOCKED LOOP BUILDING BLOCK
中文描述： 高效能雙鎖相環(huán)積木
文件頁(yè)數(shù)： 19/28頁(yè)
文件大?。?/td> 459K
代理商： TLC2942PW
TLC2942
HIGH-PERFORMANCE DUAL PHASE-LOCKED LOOP BUILDING BLOCK
SLAS146B – NOVEMBER 1996 – REVISED JUNE 1997
19
POST OFFICE BOX 655303
DALLAS, TEXAS 75265
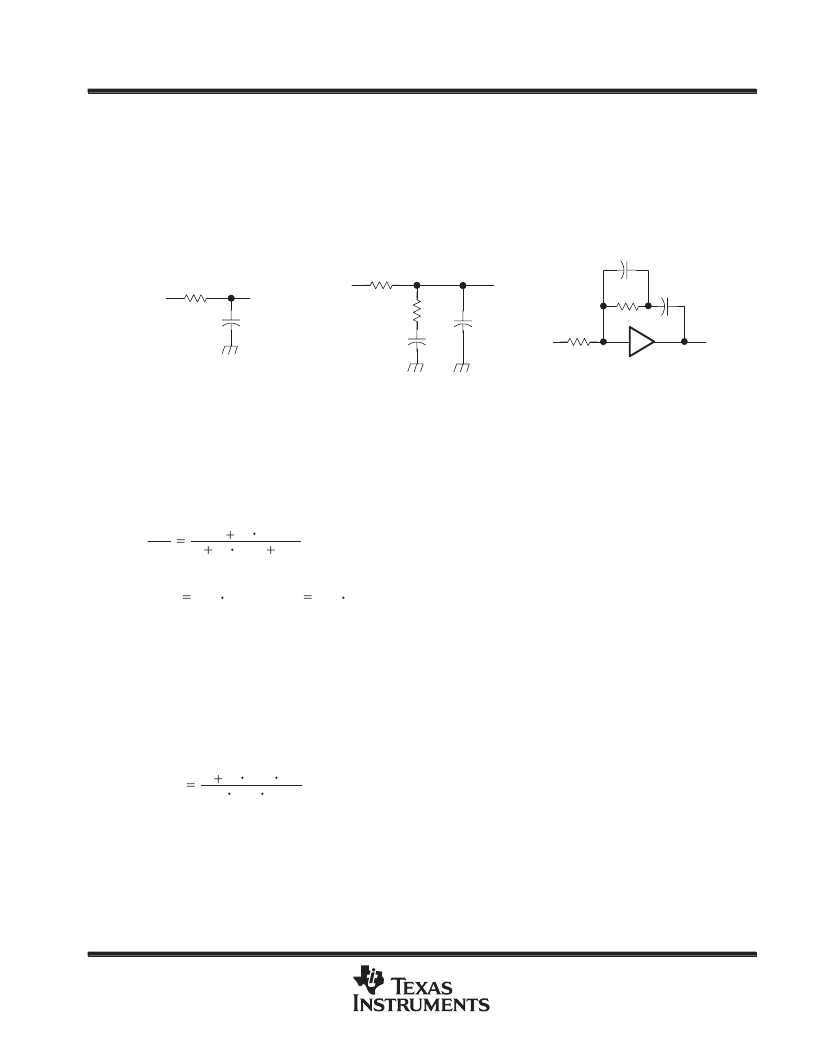
APPLICATION INFORMATION
low-pass-filter (LPF) configurations
Many excellent references are available that include detailed design information about LPFs and they should
be consulted for additional information. Lag-lead filters or active filters are often used. Examples of LPFs are
shown in Figure 25. When the active filter of Figure 25(c) is used, the reference should be applied to F
IN
-B
because of the amplifier inversion. Also, in practical filter implementations, C2 is used as additional filtering at
the VCO input. The value of C2 should be equal to or less than one-tenth the value of C1.
R1
C1
T1 = C1R1
(a) LAG FILTER
R1
C1
T1 = C1R1
T2 = C1R2
R2
(b) LAG-LEAD FILTER
R2
C1
R1
T1 = C1R1
T2 = C1R2
(c) ACTIVE FILTER
A
–
VI
VO
VI
VO
VI
C2
VO
C2
Figure 25. LPF Examples for PLL
the passive filter
The transfer function for the low-pass filter shown in Figure 25(b) is:
VO
VIN
1
s
(T1
T2
1
s
T2)
Where
T1
R1
C1 and T2
R2
C1
(2)
Using this filter makes the closed loop PLL system a type 1 second-order system. The response curves of this
system to a unit step are shown in Figure 26.
the active filter
When using the active filter shown in Figure 25(c), the phase detector inputs must be reversed since the filter
adds an additional inversion. Therefore, the input reference frequency should be applied to the F
IN
-B terminal
and the output of the VCO divider should be applied to the input reference terminal, F
IN
-A.
The transfer function for the active filter shown in Figure 25(c) is:
F(s)
1
s
R2
C1
s
R1
C1
(3)
Using this filter makes the closed loop PLL system a type 2 second-order system. The response curves of this
system to a unit step are shown in Figure 27.
相關(guān)PDF資料
PDF描述
TLC32040C ANALOG INTERFACE CIRCUITS
TLC32040I ANALOG INTERFACE CIRCUITS
TLC32041C ANALOG INTERFACE CIRCUITS
TLC32041CFN ANALOG INTERFACE CIRCUITS
TLC32041I ANALOG INTERFACE CIRCUITS
相關(guān)代理商/技術(shù)參數(shù)
參數(shù)描述
TLC2943IDB 制造商:Rochester Electronics LLC 功能描述:- Bulk
TLC-2C-0164 制造商:KATO/COILTHREAD 功能描述:
TLC-2C-0164W 制造商:KATO/COILTHREAD 功能描述:
TLC-2C-0164Y 制造商:KATO/COILTHREAD 功能描述:
TLC-2C-0246 制造商:KATO/COILTHREAD 功能描述:
發(fā)布緊急采購(gòu)，3分鐘左右您將得到回復(fù)。

采購(gòu)需求

(若只采購(gòu)一條型號(hào)，填寫(xiě)一行即可)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

發(fā)布成功！您可以繼續(xù)發(fā)布采購(gòu)。也可以進(jìn)入我的后臺(tái)，查看報(bào)價(jià)

*型號(hào) *數(shù)量 廠商 批號(hào) 封裝
添加更多采購(gòu)

我的聯(lián)系方式

*
*
*