參數(shù)資料
型號： L6917BD
廠商： 意法半導體
英文描述： 5 BIT PROGRAMMABLE DUAL-PHASE CONTROLLER
中文描述： 5位可編程雙相控制器
文件頁數(shù)： 18/27頁
文件大?。?/td> 411K
代理商： L6917BD
L6917
18/27
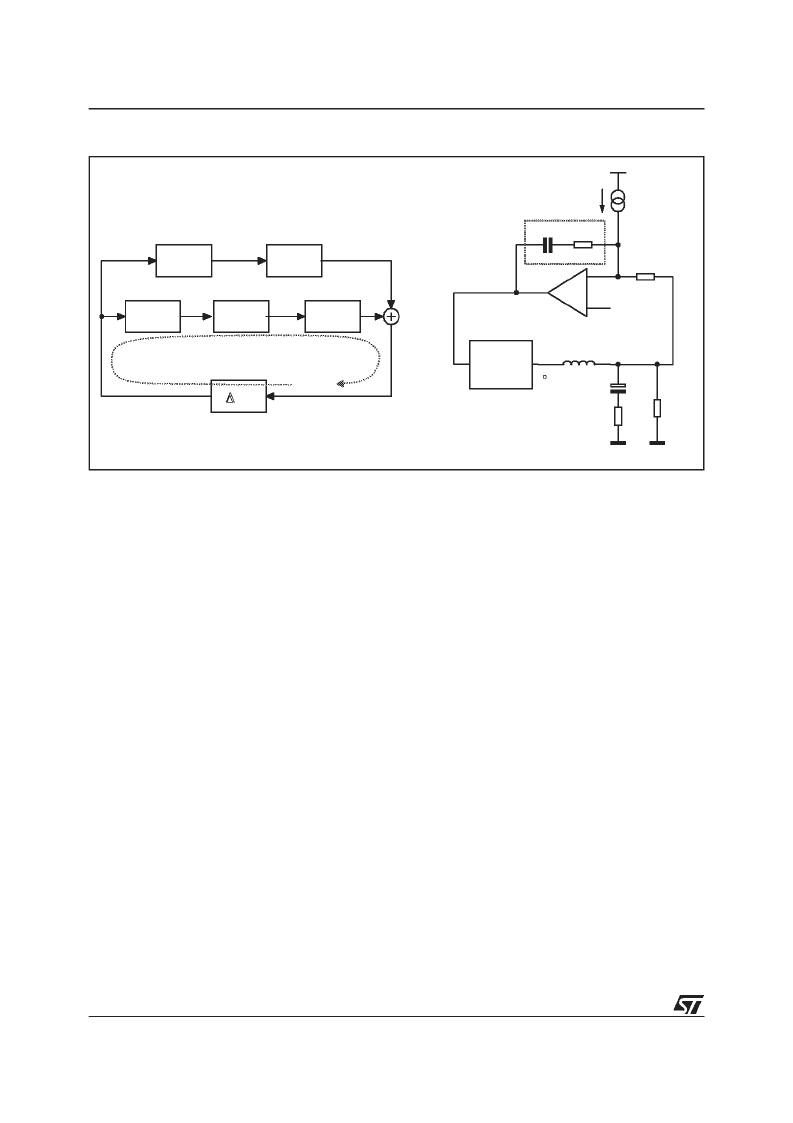
Figure 11. Control Loop Scheme
AverageCurrent Mode Compensation NetworkDesign
The average current mode control loop is reported in figure 11. The current information I
FB
sourced by the FB
pin flows into R
FB
implementing the dependence of the output voltage from the read current.
Two different loops are present and precisely a current loop internal to a voltage loop. The current gain (Ac) and
voltage gain (Av) present in the above figure are defined by the following relationships:
The current loop gain may now be expressed by the following equation:
Where
Vosc has a typical value of 2V and Z
F
(s) is the impedance of the series R
F
-C
F
. The current loop gain
is designed to obtain a high DC gain to minimize static error and cross the 0dB axes with a constant -20dB/dec
slope with a crossover frequency
ω
TI
. Neglecting the effect of Z
F
(s), the transfer function has one zero and two
poles. Both the poles are fixed once the output filter is designed and also the zero (
ω
OUT
=1/R
OUT
C
OUT
) is fixed
by the maximum current deliverable by the converter. To obtain the desired shape an R
F
-C
F
series network is
considered for the Z
F
(s) implementation. A zero at
ω
F
=1/R
F
C
F
is then introduced together with an integrator.
This integrator minimizes the static error while placing the zero in correspondence with the L-C resonance a
simple -20dB/dec shape of the gain is assured (See Figure 12).
Rout
Cout
ESR
L
R
FB
R
F
C
F
REF
PWM
I
FB
Av
-Z
F
/R
FB
Ac
Rs/Rg
-Z
F
1/
V
osc
V
COMP
V
OUT
d
V
IN
V
COMP
V
OUT
d
I
FB
I
OUT
Z
F
G
LOOPI
Av s
V
d
---------------
....
{
}
V
IN
1
s
+
ESR C
S
2
C
OUT
L
2
--
s
ESR C
OUT
2 R
OUT
-----------------------
+
1
+
+
-----------------------------------------------------------------------------------------------------------------------------
=
=
=
Ac s
I
d
------------
....
{
}
V
R
OUT
---------------
1
s
+
ESR C
S
2
C
OUT
2
--
s
ESR C
OUT
2 R
OUT
-----------------------
+
1
+
+
-----------------------------------------------------------------------------------------------------------------------------
=
=
=
G
LOOPI
s
( )
Ac s
-----------------------------------------------
Rs Z
s
( )
V
OUT
--------------
1
s
+
ESR C
S
C
OUT
2
--
s
ESR C
OUT
OUT
----------------------
+
1
+
+
------------------------------------------------------------------------------------------------------------------------------
-------
Z
s
( )
-----------------
–
=
=
相關PDF資料
PDF描述
L6917BDTR 5 BIT PROGRAMMABLE DUAL-PHASE CONTROLLER
L6OV12 Analog IC
L6OV15 Analog IC
L6OV24 Analog IC
L6OV5 Analog IC
相關代理商/技術參數(shù)
參數(shù)描述
L6917BDTR 功能描述:DC/DC 開關控制器 Prog Dual-Phase Cont RoHS:否 制造商:Texas Instruments 輸入電壓:6 V to 100 V 開關頻率: 輸出電壓:1.215 V to 80 V 輸出電流:3.5 A 輸出端數(shù)量:1 最大工作溫度:+ 125 C 安裝風格: 封裝 / 箱體:CPAK
L6917D 制造商:未知廠家 制造商全稱:未知廠家 功能描述:Analog IC
L6917DTR 制造商:未知廠家 制造商全稱:未知廠家 功能描述:Analog IC
L6918 制造商:STMICROELECTRONICS 制造商全稱:STMicroelectronics 功能描述:5 BIT PROGRAMMABLE MULTIPHASE CONTROLLER
L6918A 制造商:STMICROELECTRONICS 制造商全稱:STMicroelectronics 功能描述:5 BIT PROGRAMMABLE MULTIPHASE CONTROLLER
發(fā)布緊急采購，3分鐘左右您將得到回復。

采購需求

(若只采購一條型號，填寫一行即可)

發(fā)布成功！您可以繼續(xù)發(fā)布采購。也可以進入我的后臺，查看報價

發(fā)布成功！您可以繼續(xù)發(fā)布采購。也可以進入我的后臺，查看報價

*型號 *數(shù)量 廠商 批號 封裝
添加更多采購

我的聯(lián)系方式

*
*
*