- 您現(xiàn)在的位置:買賣IC網 > PDF目錄369509 > BT136F700E Transient Voltage Suppressor Diodes PDF資料下載
參數(shù)資料
| 型號: | BT136F700E |
| 元件分類: | TVS-瞬態(tài)抑制二極管 |
| 英文描述: | Transient Voltage Suppressor Diodes |
| 中文描述: | 可控硅| 700V的五(DRM)的| 4A條口(T)的有效值|采用SOT - 186 |
| 文件頁數(shù): | 135/224頁 |
| 文件大小: | 2697K |
| 代理商: | BT136F700E |
第1頁第2頁第3頁第4頁第5頁第6頁第7頁第8頁第9頁第10頁第11頁第12頁第13頁第14頁第15頁第16頁第17頁第18頁第19頁第20頁第21頁第22頁第23頁第24頁第25頁第26頁第27頁第28頁第29頁第30頁第31頁第32頁第33頁第34頁第35頁第36頁第37頁第38頁第39頁第40頁第41頁第42頁第43頁第44頁第45頁第46頁第47頁第48頁第49頁第50頁第51頁第52頁第53頁第54頁第55頁第56頁第57頁第58頁第59頁第60頁第61頁第62頁第63頁第64頁第65頁第66頁第67頁第68頁第69頁第70頁第71頁第72頁第73頁第74頁第75頁第76頁第77頁第78頁第79頁第80頁第81頁第82頁第83頁第84頁第85頁第86頁第87頁第88頁第89頁第90頁第91頁第92頁第93頁第94頁第95頁第96頁第97頁第98頁第99頁第100頁第101頁第102頁第103頁第104頁第105頁第106頁第107頁第108頁第109頁第110頁第111頁第112頁第113頁第114頁第115頁第116頁第117頁第118頁第119頁第120頁第121頁第122頁第123頁第124頁第125頁第126頁第127頁第128頁第129頁第130頁第131頁第132頁第133頁第134頁當前第135頁第136頁第137頁第138頁第139頁第140頁第141頁第142頁第143頁第144頁第145頁第146頁第147頁第148頁第149頁第150頁第151頁第152頁第153頁第154頁第155頁第156頁第157頁第158頁第159頁第160頁第161頁第162頁第163頁第164頁第165頁第166頁第167頁第168頁第169頁第170頁第171頁第172頁第173頁第174頁第175頁第176頁第177頁第178頁第179頁第180頁第181頁第182頁第183頁第184頁第185頁第186頁第187頁第188頁第189頁第190頁第191頁第192頁第193頁第194頁第195頁第196頁第197頁第198頁第199頁第200頁第201頁第202頁第203頁第204頁第205頁第206頁第207頁第208頁第209頁第210頁第211頁第212頁第213頁第214頁第215頁第216頁第217頁第218頁第219頁第220頁第221頁第222頁第223頁第224頁
Application Notes
AN1003
2002 Teccor Electronics
Thyristor Product Catalog
AN1003 - 3
http://www.teccor.com
+1 972-580-7777
Control Characteristics
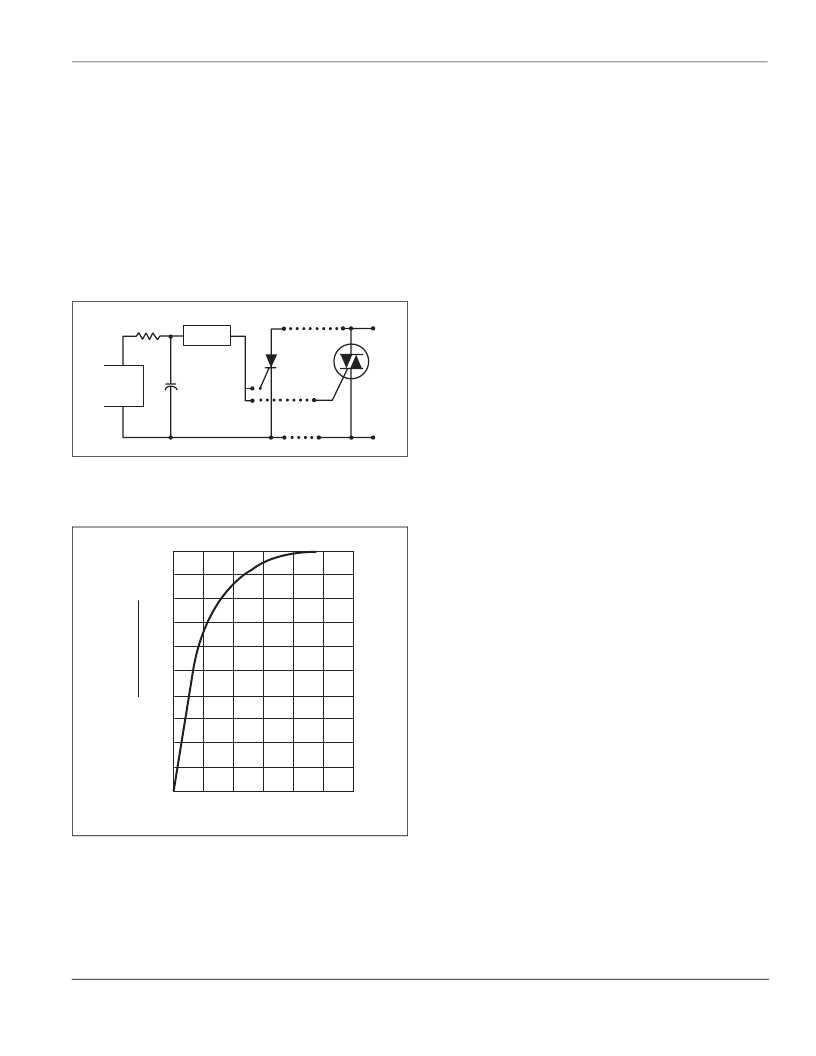
A relaxation oscillator is the simplest and most common control
circuit for phase control. Figure AN1003.7 illustrates this circuit
as it would be used with a thyristor. Turn-on of the thyristor
occurs when the capacitor is charged through the resistor from a
voltage or current source until the breakover voltage of the
switching device is reached. Then, the switching device changes
to its on state, and the capacitor is discharged through the thyris-
tor gate. Trigger devices used are neon bulbs, unijunction tran-
sistors, and three-, four-, or five-layer semiconductor trigger
devices. Phase control of the output waveform is obtained by
varying the RC time constant of the charging circuit so the trigger
device breakdown occurs at different phase angles within the
controlled half or full cycle.
Figure AN1003.7
Relaxation Oscillator Thyristor Trigger Circuit
Figure AN1003.8 shows the capacitor voltage-time characteristic
if the relaxation oscillator is to be operated from a pure DC
source.
Figure AN1003.8
Capacitor Charging from DC Source
Usually, the design starting point is the selection of a capacitance
value which will reliably trigger the thyristor when the capacitance
is discharged. Trigger devices and thyristor gate triggering char-
acteristics play a part in the selection. All the device characteris-
tics are not always completely specified in applications, so
experimental determination is sometimes needed.
Upon final selection of the capacitor, the curve shown in Figure
AN1003.8 can be used in determining the charging resistance
needed to obtain the desired control characteristics.
Many circuits begin each half-cycle with the capacitor voltage at
or near zero. However, most circuits leave a relatively large
residual voltage on the capacitor after discharge. Therefore, the
charging resistor must be determined on the basis of additional
charge necessary to raise the capacitor to trigger potential.
For example, assume that we want to trigger an S2010L SCR
with a 32 V trigger diac. A 0.1 μF capacitor will supply the neces-
sary SCR gate current with the trigger diac. Assume a 50 V dc
power supply, 30° minimum conduction angle, and 150
°
maxi-
mum conduction angle with a 60 Hz input power source. At
approximately 32 V, the diac triggers leaving 0.66 V
of diac
voltage on the capacitor. In order for diac to trigger, 22 V must be
added to the capacitor potential, and 40 V additional (50-10) are
available. The capacitor must be charged to 22/40 or 0.55 of the
available charging voltage in the desired time. Looking at Figure
AN1003.8, 0.55 of charging voltage represents 0.8 time constant.
The 30° conduction angle required that the firing pulse be
delayed 150° or 6.92 ms. (The period of 1/2 cycle at 60 Hz is
8.33 ms.) To obtain this time delay:
6.92 ms = 0.8 RC
RC = 8.68 ms
if C = 0.10 μF
then,
To obtain the minimum R (150° conduction angle), the delay is
30° or
(30/180) x 8.33 = 1.39 ms
1.39 ms = 0.8 RC
RC = 1.74 ms
0.1
×
10
Using practical values, a 100 k potentiometer with up to 17 k min-
imum (residual) resistance should be used. Similar calculations
using conduction angles between the maximum and minimum
values will give control resistance versus power characteristic of
this circuit.
Triac Phase Control
The basic full-wave triac phase control circuit shown in
Figure AN1003.9 requires only four components. Adjustable
resistor R
and C
are a single-element phase-shift network.
When the voltage across C
1
reaches breakover voltage (V
BO
) of
the diac, C
1
is partially discharged by the diac into the triac gate.
The triac is then triggered into the conduction mode for the
remainder of that half-cycle. In this circuit, triggering is in Quad-
rants I and III. The unique simplicity of this circuit makes it suit-
Switching
Device
Voltage
or
Current
Source
Triac
R
C
SCR
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
0
1
2
Time Constants
3
4
5
6
R
(
C
S
)
R
-------------------------
3
–
×
10
0.1
6
–
86,000
=
=
R
1.74
3
–
6
–
17,400
=
=
相關PDF資料 |
PDF描述 |
|---|---|
| BT136SERIES | Triacs |
| BT136SERIESD | Triacs logic level |
| BT136SERIESE | Triacs sensitive gate |
| BT136SSERIES | Triacs |
| BT136SSERIESD | Triacs logic level |
相關代理商/技術參數(shù) |
參數(shù)描述 |
|---|---|
| BT136F700G | 制造商:未知廠家 制造商全稱:未知廠家 功能描述:TRIAC|700V V(DRM)|4A I(T)RMS|SOT-186 |
| BT136F-800 | 制造商:TECCOR 制造商全稱:TECCOR 功能描述:Thyristor Product Catalog |
| BT136F-800F | 制造商:TECCOR 制造商全稱:TECCOR 功能描述:Thyristor Product Catalog |
| BT136F-800G | 制造商:PHILIPS 制造商全稱:NXP Semiconductors 功能描述:Triacs |
| BT136M | 制造商:PHILIPS 制造商全稱:NXP Semiconductors 功能描述:Triacs sensitive gate |
發(fā)布緊急采購,3分鐘左右您將得到回復。